We had a per­for­mance regression in a test suite recently when the median test time jumped by two minutes.

We tracked it down to this (simplified) code fragment:

task_inclusions = [ some_collection_of_tasks() ]
invalid_tasks = [t.task_id() for t in airflow_tasks
                 if t.task_id() not in task_inclusions]

This looks fairly in­nocu­ous—and it was—until the size of the result returned from some_­col­lec­tion_of_­tasks() jumped from a few hundred to a few thousand.

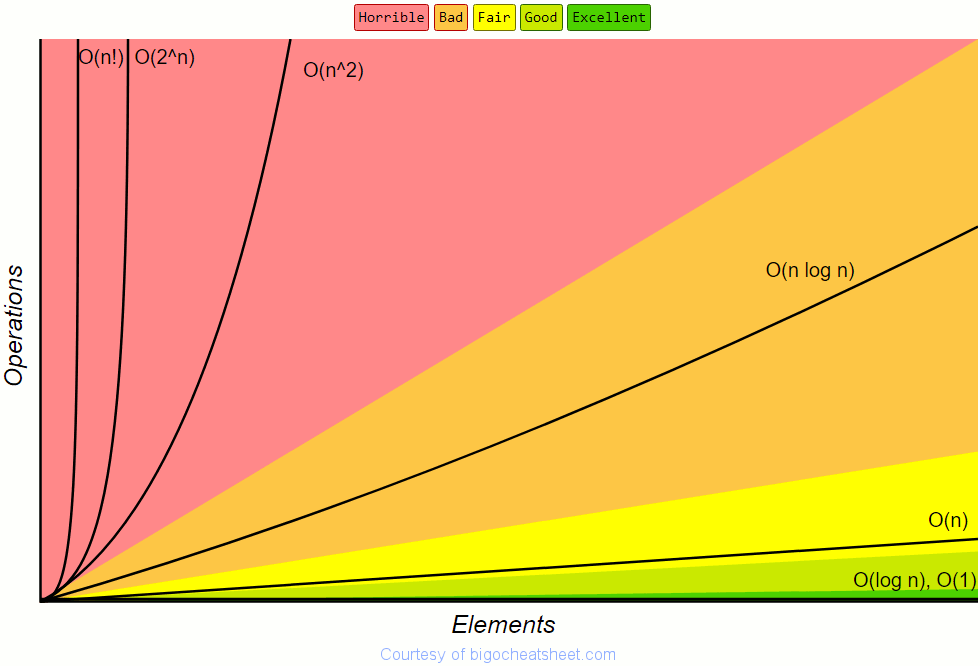
The in comparison operator con­ve­nient­ly works with all of Python’s standard sequences and col­lec­tions, but its efficiency varies. For a list and other sequences, in must search linearly through all the elements until it finds a matching element or the list is exhausted. In other words, x in some_list takes O(n) time. For a set or a dict, however, x in container takes, on average, only O(1) time. See Time Complexity for more.

The in­valid_­tasks list com­pre­hen­sion was explicitly looping through one list, air­flow_­tasks, and implicitly doing a linear search through task_in­clu­sions for each value of t. The nested loop was hidden and its effect only became apparent when task_in­clu­sions grew large.

The list com­pre­hen­sion was actually taking O(n²) time. When n was com­par­a­tive­ly small (a few hundred), this wasn’t a problem. When n grew to several thousand, it became a big problem.

This is a classic example of an ac­ci­den­tal­ly quadratic algorithm. Indeed, Nelson describes a very similar problem with Mercurial change­groups.

This per­for­mance regression was compounded because this fragment of code was being called thousands of times—I believe once for each task— making the overall cost cubic, O(n³).

The fix here is similar: Use a set instead of a list and get O(1) membership testing. The in­valid_­tasks list com­pre­hen­sion now takes the expected O(n) time.

task_inclusions = set( some_collection_of_tasks() )
invalid_tasks = [t.task_id() for t in airflow_tasks
                 if t.task_id() not in task_inclusions]

More at Un­der­stand­ing Big-O Notation and the Big-O Cheat Sheet.